Introduction
According to CDC,
"a measure of association quantifies the relationship between
an exposure and a disease among two groups."
These measures are used in epidemiological and comparative studies to assess whether there is any relationship between a factor (exposure) and a particular event. For example, you observe that people living in a certain area have higher incidence of colon cancer and that their diet predominantly consists of red meat. So, how can you assess if the high incidence of colon cancer (event) is due to red meat consumption (factor), or is it simply due to some specific genetic mutation in this population? The only way to answer such question is by comparing your observation group (exposed group) with another group which is not exposed to red meat (non-exposed group), with both groups being an accurate representation of the population of that region.
The most widely used measures of association in clinical research are Odds Ratio (OR) & Relative Ratio (RR). To understand these measure, we first grasp their underlying concept and how they are measured.
Odds Ratio (OR)
Underlying Concept: Odds
The odds of an event taking place is a ratio of how many times the event occurs to how many times the event does not occurs. To put it simply, it is the ratio of events to non-events as shown below:
The most commonly used example to explain this concept is that of a playing dice:
What are the odds of rolling 1 on a dice in a single attempt?
The chance of rolling 1 on a dice is 1
While the chance of rolling any other number is 5 (2,3,4,5,6)
So the odds of rolling a 1 would be 1 / 5 = 0.2
Odds of 0.2 - can be equated in percentage as 20%
Similarly,
What are the odds of rolling a number greater than 3 on a dice?
The chance of the event occurring is 3 (4, 5, 6)
The chance of the event not occurring is also 3 (1, 2, 3)
Therefore, the odds of rolling a number greater than 3 = 3 / 3 = 1
Odds of 1 - can be equated in percentage as 100%
How to calculate Odds Ratio (OR)?
Based on the above concept, OR is a measure which compares the odds of an event occurring after exposure to a risk factor to the odds of an event occurring in the non-exposed (control / reference) group.
Let's take the example of smoking and lung cancer as shown on our IG post.
If we want to analyze the association between exposure to cigarette smoking and occurrence of lung cancer, we need to compare the odds in the exposed (smokers) group to the non-exposed (non-smokers) group.
Where,
a = smokers with lung cancer
b = smokers without lung cancer
c = non-smokers with lung cancer
d = non-smokers without lung cancer
If we go back to our example about red meat and colon cancer, we can prepare similar tables and analyze if eating red meat is really associated with colon cancer occurrence or not.
Relative Risk or Risk Ratio (RR)
Underlying Concept: Probability
The probability of an event taking place is simply the ratio of how many times the event occurs to the number of all observations (event occurrence plus non-occurrence). To put it simply, it is the ratio of events to total events as shown below:
We can look at probability through the dice example as well:
What is the probability of rolling 1 on dice?
The chance of rolling 1 on a dice is 1
While the total number of all possible events is 6 (1,2,3,4,5,6)
So the odds of rolling a 1 would be 1 / 6 = 0.167
Probability of 0.167 - can be equated in percentage as 16.7%
Similarly
What are the odds of rolling a number greater than 3 on a dice?
The chance of the event occurring is 3 (4, 5, 6)
The total number of all possible events is 6 (1,2,3,4,5,6)
Therefore, the odds of rolling a number >3 = 3 / 6 = 0.5
Probability of 0.5 - can be equated in percentage as 50%
How to calculate Relative Risk / Risk Ratio (OR)?
Relative risk, aka Risk Ratio, is a measure which estimates the probability of an event occurring in the exposed group to the probability of an event occurring in the non-exposed (control / reference) group.
Going back to our example of smoking and lung cancer. The relative risk for this case can be calculated as shown below:
Where,
a = smokers with lung cancer
b = smokers without lung cancer
c = non-smokers with lung cancer
d = non-smokers without lung cancer
How to interpret them?
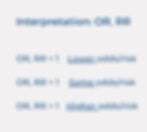
In addition, we must look at two more things:
P-value: which should reach the level of significance (usually p<alpha (0.05))
Confidence Interval: which should not include the value of 1. If it includes the value of 1, it is not a statistically significant result (for eg. CI = 0.91 to 1.29)
(more often than not, the P-value will not reach significance if the CI includes the value of 1)
When to use them?
Odds Ratio: can be calculated in any kind of study design which involves comparison between two groups.
In case-control studies and cross-sectional retrospective studies, only odds ratios can be used, since it is often difficult to acquire the actual number of all potential cases.
Risk Ratio: can only be calculated in studies in which a cause-and-effect relationship can be studied
To observe such a relationship, we need to follow the patients for a certain period of time (from exposure to the outcome/endpoint/result).
Such follow-up of patients is performed in cohort studies (prospective and retrospective) as well as in interventional studies
Therefore, RR can also be used in such studies.
Recap
For more information on measures of association, subscribe to our
EBM 101 course, where we discuss the theory behind them
EBM 201 course, where we will show you how to use statistical software to perform such analysis for your data.
Courses available in English and Polish at https://courses.houseofebm.com
Visit our Socials to stay updated about our activities, webinars, services and more:
Facebook: @houseofebm
Instagram: @house_of_ebm
Contact us at info@houseofebm.com for any enquires.